Le coefficient de corrélation linéaire permet de mesurer la liaison linéaire qui existe entre deux variables quantitatives.
Le terme de corrélation linéaire fait référence à la fonction linéaire.
Le plus usuel est le coefficient de corrélation de Pearson.
Le coefficient de corrélation linéaire est compris entre -1 et 1.
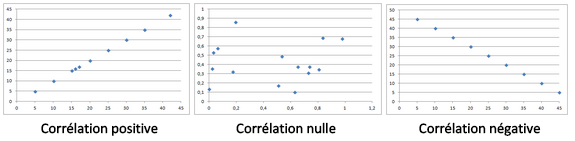
- 0 correspondant à une corrélation linéaire nulle.
- -1 une corrélation linéaire négative parfaite
- 1 une corrélation linéaire positive parfaite
Formule du coefficient de corrélation entre la variable A et la variable B:
covarianceAB / (ecart-typeA * ecart-typeB)
où covarianceAB = somme (xA - moyenneA)*(xB - moyenneB)
Il est important, voir essentiel, de tracer le nuage de points entre les deux variables étudiées.
Des exemples :
Il existe aussi d’autres coefficients de corrélation :
- celui de spearman qui compare les rangs de chaque valeur. Malheureusement, celui-ci n’est pas toujours pertinent surtout si il y a beaucoup de valeurs ex-aequo.
- celui de kendall pour chaque valeur de la première série regarde le nombre de valeurs au dessus et en dessous de la seconde série.
Attention ! le coefficient de corrélation est à manipuler avec précaution.
Le coefficient de corrélation :
- Ne détecte que les liaisons linéaires
- Un coefficient de corrélation à 0 ne signifie donc pas toujours qu’il n’y a pas de liens.
- Ne peut pas être utilisé dans tous les contextes :
- Distribution gaussienne
- Absence de valeurs extrêmes
- A besoin d’un nombre suffisant de données
Excel :
=coefficient.correlation(plageDeValeurs1;planDeValeurs2)
http://bienvenudansladata.com/site-de-rencontre-marocain-montrealSAS :
Proc corr data=votreTable; run;
http://bienvenudansladata.com/ab-coeur-site-de-rencontreR :
cor(votreVariable1,votreVariable2)
cor(votreTable) <= permet d’avoir les coefficients de corrélation pour toutes les combinaisons de variables 2 à 2.
en ajoutant l’argument use=”complete.obs” vous ignorer les individus ayant une donnée manquante pour l’une des deux variables.