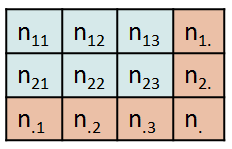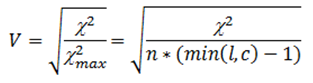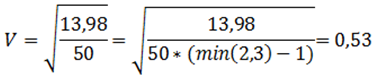Dans cet article, je vais tenter de vous expliquer le test d’indépendance du Khi 2 (ou Chi 2). Nous verrons d’abord la théorie puis un exemple pratique.
Le problème :
On souhaite savoir avec une marge d’erreur de 5% si les j populations sont identiques / ont le même comportement.
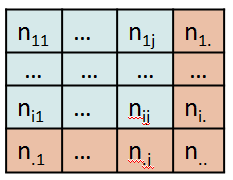
Pour ce faire, on observe un phénomène X sur j populations de taille nj.
Le phénomène X a i finalités.
On a donc le tableau de contingence suivant :
La solution :
1. Hypothèse :
Ho : les j population sont indépendantes
H1 : les j population ne sont pas indépendantes
2. Risque α =5%
3. Choix du test : Test non paramétrique d’indépendance du Khi2
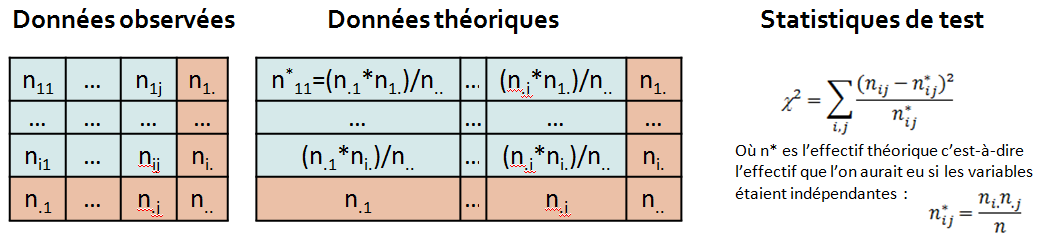
4. Statistique de test :
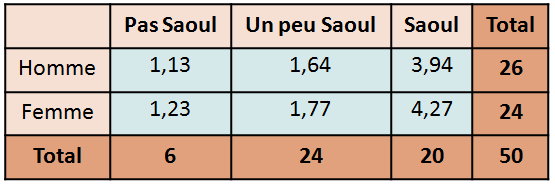
On va calculer le khi2 de notre jeu de données c’est-à-dire la distance entre les données observées et les données théoriques attendues (ici la répartition des individus dans le cas d’une indépendance).
5. La zone de rejet
Pour calculer la zone de rejet, on doit calculer le nombre de degrés de liberté.
Les degrés de liberté correspondent au nombre maximum de valeurs du modèle telles qu’aucune d’entre elle n’est calculable à partir des autres.
Dans le cas du Khi 2, on le calcule par (nombre de colonnes de la table -1 ) x (lignes-1).
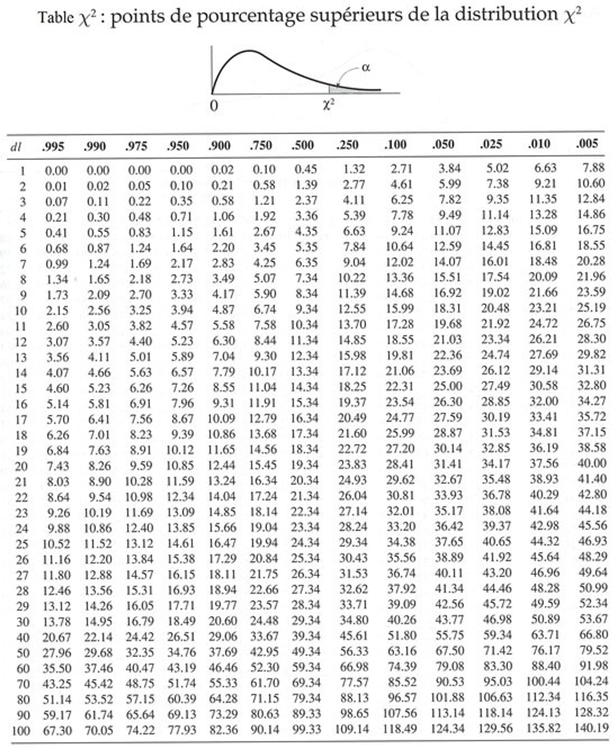
On peut trouver la valeur de comparaison grâce à cette table :
http://bienvenudansladata.com/tinder-site-de-rencontre-sinscrire
Si le khi2 calculé est supérieur à la statistique théorique, on rejette Ho.
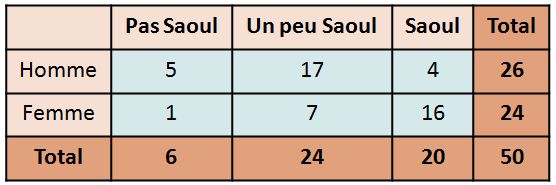
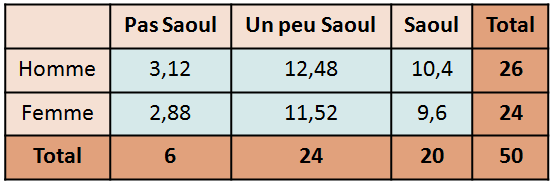
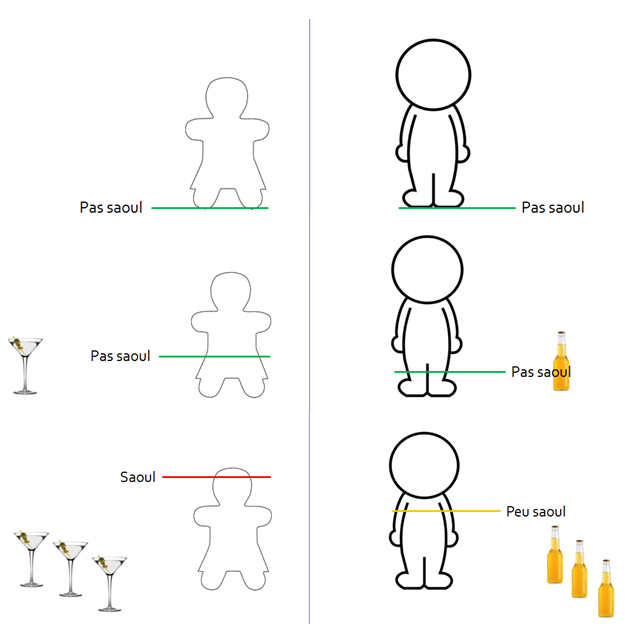
Reprenons notre exemple de lien entre le genre et l’impact de la consommation d’alcool :
http://bienvenudansladata.com/comment-rencontrer-un-homme-jeune
ddl = (3-1)*(2-1)=2
A 5%, la statistique théorique est 10,60.
On rejette donc Ho. Les deux populations sont donc dépendantes.
